AAC 841-01

Title: Aminoglycoside Nephrotoxicity: Modeling, Simulation and Control

Authors:    Florent Rougier¹, Daniel Claude², Michel Maurin³, Alexandre Sedoglavic⁴, Michel Ducher¹, Stéphane Corvaisier¹, Roger Jelliffe⁵ and Pascal Maire^1-5.

Address: (1) ADCAPT, Service Pharmaceutique, Hôpital Antoine Charial, Francheville, France. (2) Université Paris-Sud, Laboratoire des Signaux et Systèmes (CNRS-SUPELEC), Gif-sur-Yvette, France. (3) INRETS, Bron, France. (4) Laboratoire GAGE, Ecole Polytechnique, Palaiseau, France. (5) Laboratory of Applied Pharmacokinetics, University of Southern California, School of Medicine, Los Angeles CA 90033, USA.

Corresponding author: Florent Rougier, Phone: +33 472 32 34 87 Fax: +33 472 32 39 08

E-mail address: < florent.rougier@libertysurf.fr >

Correspondent Footnote: Corresponding author. Mailing address: ADCAPT, Service Pharmaceutique, Hôpital Antoine Charial, 40 avenue de la Table de Pierre, 69340 Francheville, France. Phone: +33 472 32 34 87. Fax: +33 472 32 39 08.

E-mail address: < florent.rougier@libertysurf.fr >

ABSTRACT

The main constraints to the administration of aminoglycosides are risks of nephrotoxicity and ototoxicity which can lead to acute, renal and vestibular failure. In this article we will focus on nephrotoxicity. No reliable predictor of nephrotoxicity has been found to date. We have developed a deterministic model which describes the aminoglycoside pharmacokinetic behavior (with a two compartment model), the kinetics of aminoglycoside accumulation in the renal cortex, the effect on the renal cells, the resulting effect on renal function by tubuloglomerular feedback and finally the results upon the serum creatinine concentrations. The pharmacokinetic parameter values were estimated by the NPEM program. The estimated pharmacodynamic parameter values were obtained after the minimization of the least squares objective function between measured and calculated creatinine serum levels. A simulation program assessed the influence of the dosage regimens upon the occurrence of nephrotoxicity. We show the ability of the model to fit with 49 observed creatinine serums in an 8 patient group treated for endocarditis by comparison with 49 calculated creatinine serums (r²=0.988, p<0.001). We find that for a same daily dose, nephrotoxicity observed with a thrice-daily administration schedule, appears more rapidly, induces a higher decrease of the renal function and is more prolonged than for a once-daily administration schedule. Moreover, for a once-daily administration, we have demonstrated that the time of day of administration can influence the incidence of aminoglycoside nephrotoxicity. The least nephrotoxicity was observed when aminoglycosides were administered at 01.30 p.m. Clinical application of this model might make it possible to adjust aminoglycoside dosage regimens by taking into account both the efficacy and toxicity of the drugs.

INTRODUCTION

Aminoglycoside (AG) nephrotoxicity is a well-known occurrence. However, fifty years after the discovery of the first aminoglycoside (streptomycin), nephrotoxicity is still very difficult to predict and avoid (16).

To date, no model completely describes the pharmacodynamic behavior of aminoglycoside nephrotoxicity, even though the mechanism of this toxicity has been widely studied (15, 7, 27, 4). AG are retained in the epithelial cells lining the proximal tubule after glomerular filtration. AG become attached to the brush-border membrane in their cationic form. The initial points of attachment are probably the acidic phospholipids, especially phosphatidyl-serine. In this way, aminoglycosides accumulate and cause leakage of intracellular ions (K⁺, Mg²⁺, Ca²⁺), of proteins (beta-2-microglobulin, alpha-2-macroglobulin, lysozyme) and of enzymes (alanylaminopeptidase, N-acetyl-glucosaminidase). Thus, the resulting decline of glomerular filtration has a multi-factorial origin and involves a combination of tubular and non-tubular mechanisms. The most important factor seems to be a tubuloglomerular feedback (19, 24). The kidneys have a large capacity to compensate for tubular injuries. The importance of regeneration for protection against renal injury is clearly demonstrated by the survival of laboratory rats exposed to repeated administration of high daily doses of AG (40 mg of gentamicin per kg per day for at least 42 days). After an initial episode of acute tubular necrosis that occurs within 8 to 10 days and is associated with marked azotemia, the renal function returns almost to normal, as if the kidney had become refractive (6). Regenerating cells are less differentiated and apparently less susceptible to AG (accumulation of AG is actually reduced in the cortex of animals treated for long periods).

Even though AG pharmacokinetic (PK) behavior has been accurately described in humans (22), the relation between PK and the conditions of occurrence of AG nephrotoxicity is not clearly established. Many PK studies show that at any given cumulative area under curve (AUC) of AG serum levels, the risk of nephrotoxicity is lower for once daily dosing of AG than for traditional AG dosages administered every 8 or 12 hours (1, 20, 21). This phenomenon is due to the AG renal uptake which is non-linear and saturable, as shown in animals (10) or in human studies (1, 19). Megalin explains that uptake of AG by tubule cells is saturable (23).

Unlike recent papers (20, 21), we feel that AG nephrotoxicity can be represented by a single toxicity effect model that depends neither on the AUC of AG serum levels nor on the administration schedule. We believe that a PK model alone probably cannot explain the clinical or toxic outcome without including drug distribution in a potential second compartment and/or a pharmacodynamic (PD) (effect and/or toxicity) model. Also, AG nephrotoxicity modeling must take into account both AG renal cortex amounts, the resulting PD effect represented by the cellular leakage into the renal tubule and the stimulation of the tubuloglomerular feedback that causes the decrease in glomerular filtration.

The objectives of the present article are: 1) to develop a deterministic model of AG nephrotoxicity which takes into account both PK and PD variabilities; 2) to estimate PK and for the first time PD parameters values of this model in a group of patients treated with amikacin during a long time period and 3) to simulate AG nephrotoxicity and observe the influence of the dosage regimen and the time of administration.

MATERIALS AND METHODS

Pharmacokinetic model. We chose to use a bi-compartmental pharmacokinetic model (8) with intravenous administration. The amount of AG in the serum or central compartment (Q_S(t)) (mg) depends on the AG amount coming from intravenous administration, peripheral compartments and also from renal tubular reabsorption. Q_S(t) also depends on the AG serum amount which is transferred out of the central compartment to the peripheral compartment or which is eliminated. The AG elimination rate constant can be divided into a principal renal elimination route, which depends linearly on creatinine clearance, and a non-renal elimination constant (22). Q_S(t) varies according to the following:

        (1)

with

                (2)

where i_(t) is the infusion rate (mg/h), K_i the AG non-renal elimination rate constant (1/h), K_s the renal elimination constant (ml/min/h), k_reabs the tubular reabsorption constant (1/h), CL_CR(t) the creatinine clearance (ml/min), C_(t) the AG serum concentration (mg/l), V_d the volume of distribution of AG in the central compartment (l/kg), K_cp the transfer constant from the central compartment to the peripheral compartment (1/h), K_pc the transfer constant from the peripheral compartment to the central compartment (1/h) and Q_P(t) the amount in the peripheral compartment (mg).

Pharmacodynamic model. The AG amount left in the renal cortex (Q_C(t)) is the difference between the AG amount that accumulates according to a non-linear and saturable mechanism (1, 10, 19) such as Michaelis Menten kinetics (18) as it was demonstrated in rats (10), and the AG amount which is eliminated from the renal cortex (10). Q_C(t) varies as shown below:

         (3)

where V_(t) is the maximum accumulation rate in the renal cortex (mg/h), Q_S(t) (mg) the serum amount (mg), k_M (mg) the serum amount for which V_(t)/2 is obtained and k₁ the AG elimination rate constant from the renal cortex (1/h).

The AG renal accumulation effect (E_(t)) (mM) is represented by a classic Hill equation (11, 17) which links the AG renal cortex amount to the intracellular components leaking into the renal tubule. In addition, we added a threshold of AG renal cortex amount under which no effect is observed. E_(t) varies as shown below:

if Q_C(t) < Q_min  ®  E_(t) = 0          (4)

if Q_C(t) > Q_min  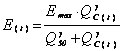®        (5)

where Q_min is the AG renal cortex amount under which no effect is observed (mg), E_max the maximum accumulation effect observed (mM), Q₅₀ the AG renal cortex amount for which E_(t) is equal to E_max/2 (mg) and g the Hill sigmoidicity parameter (dimensionless).

When the AG treatment lasts more than one month, it has been shown in the rat that despite the occurrence of nephrotoxicity during first weeks, renal function returns almost to normal from 6 or 7 weeks after the beginning of the treatment (6). The regeneration of the tubular cells during AG nephrotoxicity induces a decrease in AG renal cortex accumulation (26), i.e. a decrease in V_(t) as shown below:

     (6)

where V₀ is the maximum accumulation rate at the beginning of the treatment (mg/h) and a the maximum accumulation rate decrease constant (1/mM).

The glomerulo-tubular feedback action can also be represented by a Hill equation (24). This effect is observed on creatinine clearance (CL_CR(t)) (ml/min) and associated with a circadian variation represented here by a sinusoidal form (28) which is an independent factor. CL_CR(t) varies during a typical 24 hour day as shown below:

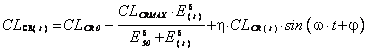     (7)

where CL_CR0 is the creatinine clearance value at the beginning of the treatment (ml/min), CL_CRMAX the maximum decrease in creatinine clearance (ml/min), E₅₀ the accumulation effect value (mM) for which CL_CR(t) is equal to CL_CRMAX/2, d the Hill sigmoidicity parameter (dimensionless), h the amplitude of the circadian variation in renal function, w the period of the circadian rhythm of the renal function (dimensionless) and j the value describing the phase relationship of the circadian rhythm (dimensionless).

The decrease in renal function involves a rise in serum creatinine which depends on the muscular daily production and the daily renal elimination (13). The serum creatinine amount (SCr_(t)) (mg) varies as shown below:

       (8)

where CL_CR(t) is the creatinine clearance value (ml/min), Vol the volume of distribution of creatinine (l) and k₂ the mean value of muscular daily creatinine production (mg/h).

Model development. We used the Matlab^Ò-Simulink^Ò program (the Math Works Inc.) for all the simulations and estimations. The program makes it possible to select each PK and PD parameter value. The inputs of the system are represented by a choice in administration schedule with the possibility to enter a first loading dose, the number of doses, the infusion time, the infusion hour and the delay between two infusions. Every simulation began at 0.00 a.m. The glomerular filtration rate shows a repeating pattern of variation over 24 hours, i.e. a circadian rhythm (14). This corresponds to an w value of 2p/24 (EQ.7). We chose a sinusoidal adjustment so that the creatinine clearance value was highest at 2.00 p.m. and lowest at 2.00 a.m. (14). This corresponds to a j value of -2p/3 (EQ.7). The amplitude of the circadian rhythm was fixed at 10% (h=0.1) (EQ.7) of the creatinine clearance value which is the most widespread value (14).

Experimental framework. For the PK and PD parameter estimations, we used data from patients for whom renal toxicity had been observed as shown by an increase in the creatinine serum levels (i.e. a decrease in creatinine clearance) without any other clinical explanation. The large number of parameters to be estimated led us to select patients who had a large number of measures of creatinine serum levels, i.e. patients treated over a long period. Eight patients treated with amikacin and vancomycin for over one month, corresponding to patients treated for endocarditis, were selected. The patients’ general characteristics and the treatment conditions are described in Table 1. Amikacin was administered once-daily with 30-minute infusions. Vancomycin was administered twice-daily during the first 2-3 days of the treatment and then once-daily after with 2-hour infusions. Amikacin doses were calculated in function of initial creatinine clearance value (CL_CR0) i.e. 15 mg/kg/j when CL_CR0 was above 80 ml/min and 7.5 mg/kg/j when CL_CR0 was between 30 and 80 ml/min. Doses of amikacin and vancomycin were constant and not adapted during the treatment. Except vancomycin, none other nephrotoxic drug was administered during the amikacin treatments. The creatinine serum levels were measured at different times of the treatment and also after it was ended, in order to observe the overall evolution of the kinetics of the serum creatinine levels.

PK and PD parameter values for estimations and simulations. For the estimations, the K_i parameter value (EQ.1) was fixed at 0.006932 1/h which corresponds to the K_i value observed for anuric patients (half-life of 100 hours) (12). We have chosen to fixe the K_i parameter value in order to put the whole variability of elimination on K_s because non-renal elimination is very small in comparison with K_s. The k_reabs parameter value was fixed at 0.05 (dimensionless) (12) otherwise the system is not identifiable. Others individual PK parameter values (K_s, V_d, K_cp and K_pc) were estimated by the NPEM program (25). Concerning PD parameter values, E₅₀ was fixed at 33.5 mM (24) otherwise a and E_max are not identifiable. Moreover V₀ was fixed at 1 mg/h in order to obtain Q_c(t) values in the range of bibliographic data (10), otherwise Q₅₀ is not identifiable. Others PD parameters (k_M, k₁, Q_min, E_max, Q₅₀, g, CL_CRMAX, d, a, k₂ and Vol) were estimated from the 8 patient group with the Matlab^Ò program by using the PK parameter values estimated, the fixed PD parameter values described above (E₅₀ and V₀) and by minimizing the least squares objective function (OF) as shown below:

    (9)

where OF is the objective function to minimize, SCr_obs the measured creatinine serum level (mg/l) and SCr_calc the calculated creatinine serum level (mg/l).

The parameters values used for simulations are those described in Table 2. PK parameters (K_i, K_s, V_d, K_cp, K_pc and k_reabs) correspond to bibliographic data (12). a was defined so that renal function returns almost to normal after 42 days of amikacin treatment with 1000 mg per day, which is the delay observed in the rat (6): that corresponds to an a value equal to 0.02 mM^-1. Others PD parameter values were mainly drawn from past studies and were the following: V₀ and k_M (10), CL_CRMAX, E₅₀ and d (24), k₂ and Vol (13). In the absence of bibliographic data, others PD parameter values (k₁, Q_min, E_max, Q₅₀ and g) were those estimated with the Matlab program in the 8 patient group. The initial creatinine clearance (CL_CR0) and creatinine serum level (SCr₀) were respectively fixed at normal values i.e. 100 ml/min and 8 mg/l.

RESULTS

The fit of the data with the model. Table 2 shows medians, minima and maxima of PK parameter values (V_d, K_s, K_cp and K_pc) estimated by the NPEM program with a two-compartment model. Table 2 also describes medians, minima and maxima of PD parameter values (k_M, k₁, Q_min, E_max, Q₅₀, g, CL_CRMAX, d, a, k₂ and Vol) estimated for the 8 patients by minimizing the objective function (EQ.9) with the Matlab^Ò program.

Figure 1 shows the relation between 49 observed creatinine serum levels and 49 calculated creatinine serum levels, represented by a linear regression with a high and significative correlation coefficient value (r²=0.9884, p<0.001) and the absence of bias (p<0.01).

Simulations. Figure 2 shows the simulated difference between the amounts of amikacin in the renal cortex for 3 different infusion schedules, with an identical cumulative AUC of amikacin serum levels, administered over a 30-day period with identical daily doses (800 mg). The doses were: 1600 mg every 48 hours; 800 mg once daily and 267 mg three times daily. The infusion time was fixed at 30 minutes for all administration doses. Figure 2 shows the lowest renal cortex accumulation and therefore the lowest decrease in creatinine clearance when amikacin is administered less frequently. Figure 2 shows that with a more frequent dosage regimen, nephrotoxicity: 1) appears more rapidly, 2) induces a higher decrease of the renal function and 3) is more prolonged. Figure 3 shows the influence of different k_m values on the AG renal accumulation with a same dosage regimen i.e. 1000 mg per day of amikacin during a 30-day period. The lower the k_m, the higher accumulation is observed (Q_c=106.26 mg for k_M=1 mg, Q_c=99.52 mg for k_M=5 mg, Q_c=86.08 mg for k_M=15 mg and Q_c=68.08 mg for k_M=30). Figure 4 only describes the influence of the time of day of administration due to the circadian variation of the renal function (01.30 p.m. versus 01.30 a.m.) with a 30-day amikacin treatment (1000 mg once-daily). The least nephrotoxicity is obtained when amikacin is administrated at 01.30 p.m. The PK and PD parameter values for all simulations are those described in Table 2.

DISCUSSION

Many methods have been proposed to reduce AG nephrotoxicity. Molecular modeling can bring about an intrinsically less toxic AG (19) but these methods are very expensive. Protective approaches such as the administrations of polyaspartic acid or deferroxamine can reduce AG renal injuries. Unfortunately, these approaches could not be translated into clinical applications because of a lack of efficacy and/or intrinsic toxicity (19). In addition, population PK computer programs, used to control AG serum levels, are good predictors of efficacy as they calculate PD indices such as AUC/MIC or C_max/MIC ratio (3). By contrast, the estimated concentrations in the second compartment are not good predictors of nephrotoxicity because they do not take into account non-linear processes such as the AG uptake in the renal cortex or the tubuloglomerular feedback. Then, a new methodology more suitable for clinical practice was developed. This methodology is based on a PK/PD model. A Deterministic model seems to be sufficient to represent AG nephrotoxicity. Our model is complex because it takes into account the renal physiology and describes most precisely the mechanisms involved in AG nephrotoxicity. This approach is very interesting because it gives much information about PK and PD behaviors of AG in individual patients.

The high and significative coefficient correlation value (r²=0.9884, p<0.001) and the absence of bias (p<0.01) (figure 1) show that our model is a powerful tool to represent the AG renal injuries. It might be useful to predict the occurrence of AG nephrotoxicity.

Goldbeter and Claude show that the modeling approach can explain the influences of time-patterned drug administration on toxicity in general (9). AG nephrotoxicity can be influenced by the administration schedule (5), by the hours of administration (2) by the parameter k_M (EQ.3) (10) and by inter and intra-individual variabilities (16). All these aspects are explored here below.

For an identical amikacin total dose, the cumulative AUC of amikacin serum levels remained unchanged for all administration schedules, but the amikacin renal cortex amounts differed from each other (figure 2A). As is well known (21), less toxicity is observed when administrations are less frequent (figure 2B) while the efficacy remains the same (the AUC of the AG serum levels and the AUC/MIC ratio remain unchanged). In addition, our model shows that nephrotoxicity: 1) appears more rapidly, 2) induces a higher decrease of the renal function and 3) is more prolonged when administration schedules are more frequent (figure 2B). Accordingly, the difference in reduction of creatinine clearance between the 3 dosage regimens for an identical daily dose is maximum on day 30. On that day, the creatinine clearance still represents 99% of the initial creatinine clearance for the 1600 mg every 48 hour dosage regimen versus only 82% for the 267 mg three times daily dosage regimen. Although less frequent administrations entail a lesser AG renal cortex amount, the resulting effects on the renal function can be very close to each other because of non-linear relationships. Hence, very similar effects can be observed and the ability to select a less frequent dosage regimen in order to obtain a lesser toxicity is not established when the treatments are prolonged.

Because the AG uptake on renal cells is saturable (10, 27), the AG renal cortex amount is also saturable. The more quickly saturated it is (i.e. the lower the k_M) (EQ.3) the less the AG renal cortex amount is affected by peak serum levels (figure 3). However, the lower the saturability level (i.e. the lower the k_M) the less renal protection is observed (figure 3). When the k_M is lower the amikacin renal cortex amount increases. When the k_M is higher the amikacin renal cortex amounts decreases. In fact, 1/k_M can be considered as an index of sensibility of the patient for the drug. The higher the k_M, the lower the sensibility, the lower renal cortex accumulation and the lower the nephrotoxicity. Patients with a high k_M value are less sensitive to AG nephrotoxicity.

In accordance with Beauchamp and Labrecque, our model shows that AG administration at 01.30 p.m., i.e. during activity period or food intake, is preferable to an administration at 01.30 a.m., i.e. during the rest period as it was demonstrated in humans or in animals (2). The mechanisms associated with temporal variations in the AG nephrotoxicity are not completely understood but two hypotheses can be given. First, temporal variations of PK parameters and second, food intake or activity period may be of crucial importance (2). The relation between food intake and the interactions of aminoglycosides with renal tubular cells seems to be linked with the urine pH (2). The interaction will be stronger at low pH than at high pH, since these molecules will be fully protoned at low pH. It has been shown that urine pH is higher during the activity period or during the period of food intake and lower during the rest period (2). This could partly explains the lower nephrotoxicity during the activity period. Our model confirms that a simple change of the administration time (01.30 p.m. instead of 01.30 a.m.) for an identical dosage, causes from day 8 a decrease in toxicity quantified by the difference between the two evolutions of the creatinine clearance values (figure 4). The administrations at 01.30 a.m. induce a higher renal cortex accumulation and therefore a higher nephrotoxicity. The difference between the two creatinine clearance evolutions is positive and becomes maximum at day 16 (5.7 ml/min). After that, the difference in toxicity decreases until the treatment is stopped at day 30. This phenomenon may be explained by the fact that the diminution of the creatinine clearance follows a non-linear process. To two very different AG renal cortex amounts correspond two very similar effects on the creatinine clearance when the CL_CRMAX value -i.e. the maximum diminution of the creatinine clearance- is attained (EQ.7). After the end of the treatment at day 30, a lower reduction of creatinine clearance is still observed when AG is administered at 01.30 p.m. In fact, over time, renal function returns to its initial value for both administration schedules but more rapidly so with a daily administration at 01.30 p.m. After the treatment is stopped, whenever AG renal cortex amounts are lower when AG is administered at 01.30 p.m. as against administration at 01.30 a.m., this induces a lesser decrease in creatinine clearance. The difference between the two creatinine clearance evolutions is maximum at day 32 (6.2 ml/min), i.e. 2 days after the end of the treatment; then, it decreases to zero at day 35, i.e. 5 days after the end of the treatment. It corresponds to the required time for a complete elimination of AG renal cortex amounts. At that date, the creatinine clearance values are equal to those observed before the beginning of the treatment because AG nephrotoxicity is reversible, as is well known (19).

The deterministic aspect of this non-linear model is particularly shown on figure 4. That concerns the periodic oscillations (period of 24 hours) corresponding to the administration schedules. Hence, we are in the presence of a non-linear deterministic model (but not stochastic) forced by periodic oscillations.

Some PD parameters estimated for 8 patients treated with amikacin for endocarditis during a long period, show a higher variability than others (Table 2). The great variability observed during the AG nephrotoxicity (16) is partly due to the interindividual variability in renal cortex accumulation (EQ.3), especially for parameters k_M (53%) and k₁ (50%) (Table 2). Another source of interindividual variability is the resulting effect of the renal cortex accumulation, i.e. the leaking of intracellular components into the renal tubule through the E_max (110%) and Q₅₀ (81%) parameters. Some other PD parameters show a slight interindividual variability, such as CL_CRMAX (37%) and d (18%) which are tubuloglomerular feedback parameters. These results may explain why some patients are more sensitive to AG nephrotoxicity than others. In fact, high interindividual variability is observed for parameters linked to the AG itself. By contrast, a small interindividual variability is observed for the physiological process that induces a decrease in renal function. The model also takes into account intra-individual variability, i.e. a change of the parameter values during a treatment. For example, intra-individual variability can be observed in some clinical situations when the infection itself induces a decrease in renal function. When the infection is treated, the renal function is restored. In addition, experimental studies show that the accumulation of gentamicin is actually reduced in the cortex of animals treated for long periods of time by a mechanism that involves a decrease in AG renal accumulation rate, i.e. a decrease in V_(t) (EQ.6) (26).

One of the most interesting aspects of this deterministic model is that it makes it possible, for the first time, to estimate some PD parameter values with the help of creatinine serum levels. However, in clinical routine, the utilization of creatinine serum levels as a marker of renal function is not 100% reliable. In fact, creatinine serum levels increase only when renal mechanisms fail to compensate for all the toxicity. In short, the creatinine serum level is a belated marker of the renal function. The utilization of an early marker of renal injuries like enzymuria (alanylaminopeptidase) as a complement to the creatinine serum levels is necessary to better estimate the PD parameter values, chiefly those with great interindividual variability.

This deterministic model, as presented in this article, is a powerful tool to simulate and control AG nephrotoxicity. Its utilization brings rationality to empirical observations established in the past 50 years. These results could be confirmed by the joint utilization of an efficacy model (such as Zhi model (29) or others) and the toxicity model described in this article. The population PK computer programs do not make it possible to achieve an overall optimum therapy. The aim of any therapy is to obtain the highest efficacy short of exceeding toxicity limits. In future, it might not be idle to consider entering this model into the population PK programs, which would enable them to achieve this type of optimization.

REFERENCES

1. Barclay, M. L., C. M. J. Kirkpatrick, and E. J. Begg. 1999. Once-daily aminoglycoside therapy. Is it less toxic than multiple daily doses and how should it be monitored? Clin. Pharmacokinet. 36:89-98.

2. Beauchamp D., G. Labrecque. 2001. Aminoglycoside Nephrotoxicity: do time and frequency of administration matter? Curr. Opin. Crit. Care. 7(6):401-408.

3. Corvaisier, S., P. H. Maire, M. Y. Bouvier d’Yvoire, X. Barbaut, N. Bleyzac, and R. W. Jelliffe. 1998. Comparison between Antimicrobial Pharmacodynamic Indices and Bacterial Killing as Described by using the Zhi Model. Antimicrob. Agents Chemother. 42:1731-1737.

4. De Broe, M.E., G.J. Paulus, G. Verpooten, F. Roels, N. Buyssens, R. Wedeen, and P.M. Tulkens. 1984. Early effects of gentamicin, tobramycin and amikacin on the human kidney. Kidney Int.. 25:643-652.

5. De Broe, M. E., and G. A. Verpooten. 1991. Influence of dosage schedules on renal accumulation of amikacin and tobramycin in man. J. Antimicrob. Chemother. 27(suppl C):41-47.

6. Elliott, W. C., D.C Houghton, D.N. Gilbert, J. Baines-Hunter, and W.M. Bennett. 1982. Gentamicin nephrotoxicity. I. Degree and permanence of acquired insentivity. J. Lab. Clin. Med. 100:501-512.

7. Evan, A.P., and Luft F.C. 1982. Néphrotoxicité, ototoxicité médicamenteuses. Edition INSERM. Gentamicin-induced glomerular injury. p 67-78.

8. Gibaldi M., Perrier D. 1991. Drug and pharmaceutical sciences: Pharmacokinetics, vol. 15, 2^nd ed. M. Dekker Inc, New York.

9. Goldbeter, A., and D. Claude. 2002. Time-patterned drug administration: Insights from a modelling approach. Chronobiol. Int. 19(1):157-175.

10. Guiliano, R. A., G. A. Verpooten, L. Verbist, R. P. Wedeen, and M. E. De Broe. 1986. In vivo uptake kinetics of aminoglycosides in the kidney cortex of rats. J. Pharmacol. Exp. Ther. 236:470-475.

11. Hill A.V. 1910. The possible effects of the aggregation of hemoglobin on its dissociation curve. J. Physiol. 40:iv-vii.

12. Hurst, A.K., K.T. Iseri, M.A. Gill, J.K. Nogushi, T.M. Gilman, and R.W. Jelliffe. 1987. Comparison of four methods for predicting serum gentamicin concentrations in surgical patients with perforated or gangrenous appendicitis. Clin. Pharmacy. 6:234-238.

13. Jelliffe, R.W., and S. Jelliffe. 1972. A computer program for estimation of creatinine clearance from unstable serum creatinine levels. Math. Biosci. 14:17-24.

14. Koopman, M.G., G.C. Koomen, R.T. Krediet, E.A. de Moor, F.G. Hoek, and L. Arisz. 1989. Circadian rythm of glomerular filtration rate in normal individuals. Clin. Sci. 77(1):105-111.

15. Kosek, J.C., R.I. Mazze, and J. Cousins. 1974. Nephrotoxixity of gentamicin. Lab. Invest. 30:48-57.

16. Maire, P.H., S. Corvaisier, F. Rougier, M. Bouvier D'Yvoire, D. Claude, X. Barbaut, G. Carret, F. Jehl, M. Ducher, and R.W. Jelliffe. 2000. Précis de bactériologie clinique, edition ESKA, Chap. 35 Pharmacocinétique / Pharmacodynamie clinique des antibiotiques, p. 715-731.

17. Maurin, M., F. Rougier, and P. Maire. 2000. Note de calcul sur les lois de Hill : aspects probabiliste déterministe et épistémologique. Edition INRETS-LTE 2026. ISRN: INRETS/NST/00-548-FR.

18. Michaelis, L., and M.L. Menten. 1913. Die kinetik der Invertinwirkung. Biochemische Zeitschrift. 49:333-369.

19. Mingeot-Leclerq, M. P., and P. M. Tulkens. 1999. Aminoglycosides: Nephrotoxicity. Antimicrob. Agents Chemother. 43:1003-1012.

20. Murry, K. R., P. S. McKinnon, B. Mitrzyk, and M. J. Rybak. 1999. Pharmacodynamic characterization of nephrotoxicity associated with once-daily aminoglycoside. Pharmacotherapy. 19:1252-1260.

21. Rybak, M. J., B. J. Abate, S. L. Kang, M. J. Ruffing, S. A. Lerner, and G. L. Drusano. 1999. Prospective evaluation of the effect of an aminoglycoside dosing regimen on rates of observed nephrotoxicity and ototoxicity. Antimicrob. Agents Chemother. 43:1549-1555.

22. Schentag, J.J. 1977. Renal clearance and tissue accumulation of gentamicin. Clin. Pharmacol. Ther. 22:364-370.

23. Schmitz, C., J. Hilpert, C. Jacobsen, C. Boensch, E.I. Christensen, F.C. Luft, and T.E. Willnow. 2002. Megalin deficiency offers protection from renal aminoglycoside accumulation. J. Biol. Chem., 277(1):618-622.

24. Schnermann, J., D.A. Häberle, J.M. Davis, and K. Thurau. Renal Physiology. Oxford University Press, 1992. Chap. 34 Tubuloglomerular feedback control of renal vascular resistance, p. 1775-1705.

25. Schumitzky A. 1991. Nonparametric EM algorithms for estimating prior distributions. Appl. Math. Comput., 45:143-157.

26. Sundin, D. P.,C. Meyer, R.Dahl, A. Geerdes, R. Sandoval, and B. A. Molitoris. 1997. Cellular mechanism of aminoglycoside tolerance in long term gentamicin treatment. Am. J. Physiol., 41:C1309-C1318.

27. Tulkens, P.M. 1989. Nephrotoxicity of aminoglycosides. Toxicol. Lett., 46:107-123.

28. Ware J.H., and R.E. Bowden. 1977. Circadian rhythm analysis when output is collected at intervals. Biometrics. 33(3):566-571.

29. Zhi, J., Nightingale C.H., and Quintilini R. 1986. A pharmacodynamic model for the activity of antibiotics against microorganisms under nonsaturable conditions. J. Pharm. Sci. 75:1063-1067.

LEGENDS FOR FIGURES

Figure 1. Comparison between observed (SCr_obs) and calculated creatinine serum levels (SCr_calc) (n=49) in an 8 patient group treated during a long period for endocarditis. Different symbols have been used for each patient.

Figure 2. Evolution of amikacin renal cortex amounts corresponding to 3 different dosage regimens with an identical total dose (A) and resulting effects on mean renal function evolution (B).

Figure 3. Comparison of AG renal cortex amount evolutions for different possible values of k_m for an amikacin treatment with 1000 mg once daily during a 30 day-period.

Figure 4. Difference between the two creatinine clearance evolutions of two dosage regimens with 1000 mg of amikacin once daily over a 30 day-period when amikacin is administered at 01.30 p.m. or at 01.30 a.m.

TABLE 1. General characteristics of 8 patients treated with amikacin and vancomycin over a long time period for endocarditis and used for estimations.

                    ^a Initial value of creatinine clearance.

TABLE 2. Pharmacokinetic and pharmacodynamic parameter values used for simulations and estimated values (median, max, min) for 8 patients treated over a long period.

^a Equation in parenthesis are those describes in Materiel and Method.

^b Parameter values for all the simulations. Bibliographic reference in parenthesis.

^c For 8 patients treated over a long period (>1month) for endocarditis.

 Retour au menu précédent